Workshop R & RStudio

class: title-slide, center, middle

<style>

.center2 {
  margin: 0;
  position: absolute;
  top: 50%;
  left: 50%;
  -ms-transform: translate(-50%, -50%);
  transform: translate(-50%, -50%);
}

.rcorners1 {
  margin: auto;
  border-radius: 25px;
  background: #ada500;
  padding: 10px;
#  width: 50%;
}
</style>

.remark-code, .remark-inline-code { font-family: 'Source Code Pro', 'Lucida Console', Monaco, monospace;
                                    font-size: 90%;
                                  }

</style>

# ICO Workshop R & RStudio
.font160[
.SW-greenD[Part 5]
]
.font120[
.SW-greenD[*Statistical analyses in*] .UA-red[*`R`*]
]
Sven De Maeyer & Tine van Daal

.font80[
.UA-red[
2nd - 4th July, 2024
]
]

---
class: inverse-green, left

# Overview

.center2[

- Correlation --- ([Click here](#part1))
- t-test --- ([Click here](#part2))
- Linear regression --- ([Click here](#part3))
]

---
class: inverse-green, center, middle
name: part1

# 1. Correlation

---

## The .UA-red[`cor( )`] function

.pull-left[
<img src="Slides_Part5_files/figure-html/unnamed-chunk-2-1.png" width="360" />
]

.pull-right[
.UA-red[Watch out for NA's!!]
.footnotesize[

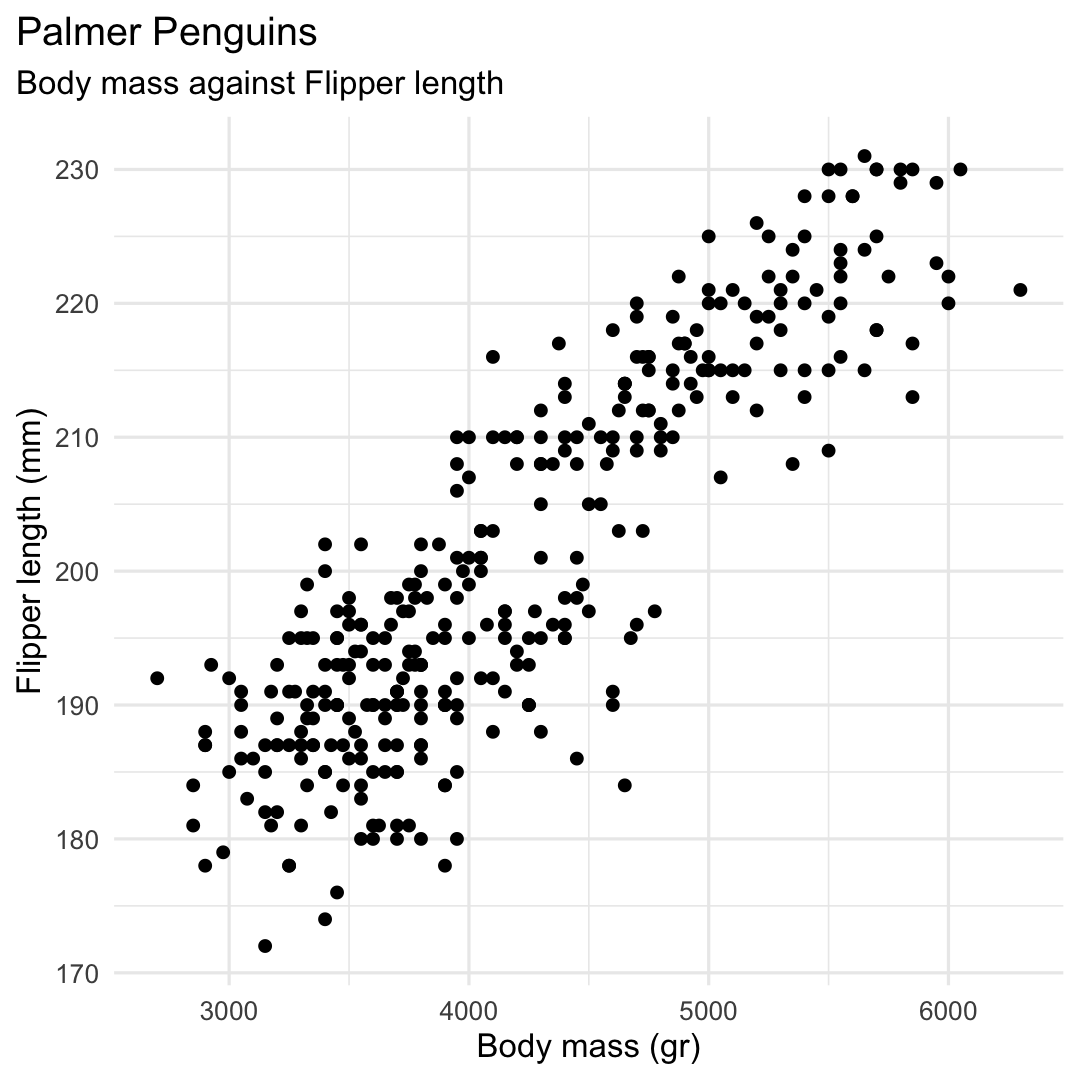
```r
library(palmerpenguins)
data("penguins")

cor(penguins$flipper_length_mm, 
    penguins$body_mass_g)
```

```
## [1] NA
```

```r
cor(penguins$flipper_length_mm, 
    penguins$body_mass_g, 
   use = "complete.obs")
```

```
## [1] 0.8712018
```
]
]

---

## Statistical tests with .UA-red[`cor.test( )`]

```r
cor.test(penguins$flipper_length_mm, 
        penguins$body_mass_g)
```

```
## 
## 	Pearson's product-moment correlation
## 
## data:  penguins$flipper_length_mm and penguins$body_mass_g
## t = 32.722, df = 340, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.843041 0.894599
## sample estimates:
##       cor 
## 0.8712018
```

---
<div class="my-logo-right"> <img src="broom_logo.png" width="100%"/> </div>

## The .UA-red[`broom`]  package

- Package in `tidyverse`

- Creates .SW-greenD[**tibbles**] based on results from a statistical analysis!

.UA-red[`tidy()`]: output from an analysis as a tibble

```r
library(broom)
C <- cor.test(penguins$flipper_length_mm, 
        penguins$body_mass_g)

tidy(C)
```

```
## # A tibble: 1 × 8
##   estimate statistic   p.value parameter conf.low conf.high method   alternative
##      <dbl>     <dbl>     <dbl>     <int>    <dbl>     <dbl> <chr>    <chr>      
## 1    0.871      32.7 4.37e-107       340    0.843     0.895 Pearson… two.sided
```

---

## Correlation between multiple variabeles

```r
penguins %>% 
  select(
    bill_depth_mm,
    bill_length_mm,
    flipper_length_mm,
    body_mass_g
  ) %>%
  cor(use = "pairwise.complete.obs")
```

```
##                   bill_depth_mm bill_length_mm flipper_length_mm body_mass_g
## bill_depth_mm         1.0000000     -0.2350529        -0.5838512  -0.4719156
## bill_length_mm       -0.2350529      1.0000000         0.6561813   0.5951098
## flipper_length_mm    -0.5838512      0.6561813         1.0000000   0.8712018
## body_mass_g          -0.4719156      0.5951098         0.8712018   1.0000000
```

---

## Correlations between multiple variabeles visualized

.pull-left[
Package: .UA-red[`GGally`]

Function: .UA-red[`ggpairs()`]

Result: a ggplot object...

.footnotesize[

```r
library(GGally)
penguins %>% 
  select(
    species,
    bill_depth_mm,
    bill_length_mm,
    flipper_length_mm,
    body_mass_g
  ) %>%
  ggpairs(
    columns = c(
      "flipper_length_mm", "body_mass_g",
      "bill_length_mm", "bill_depth_mm")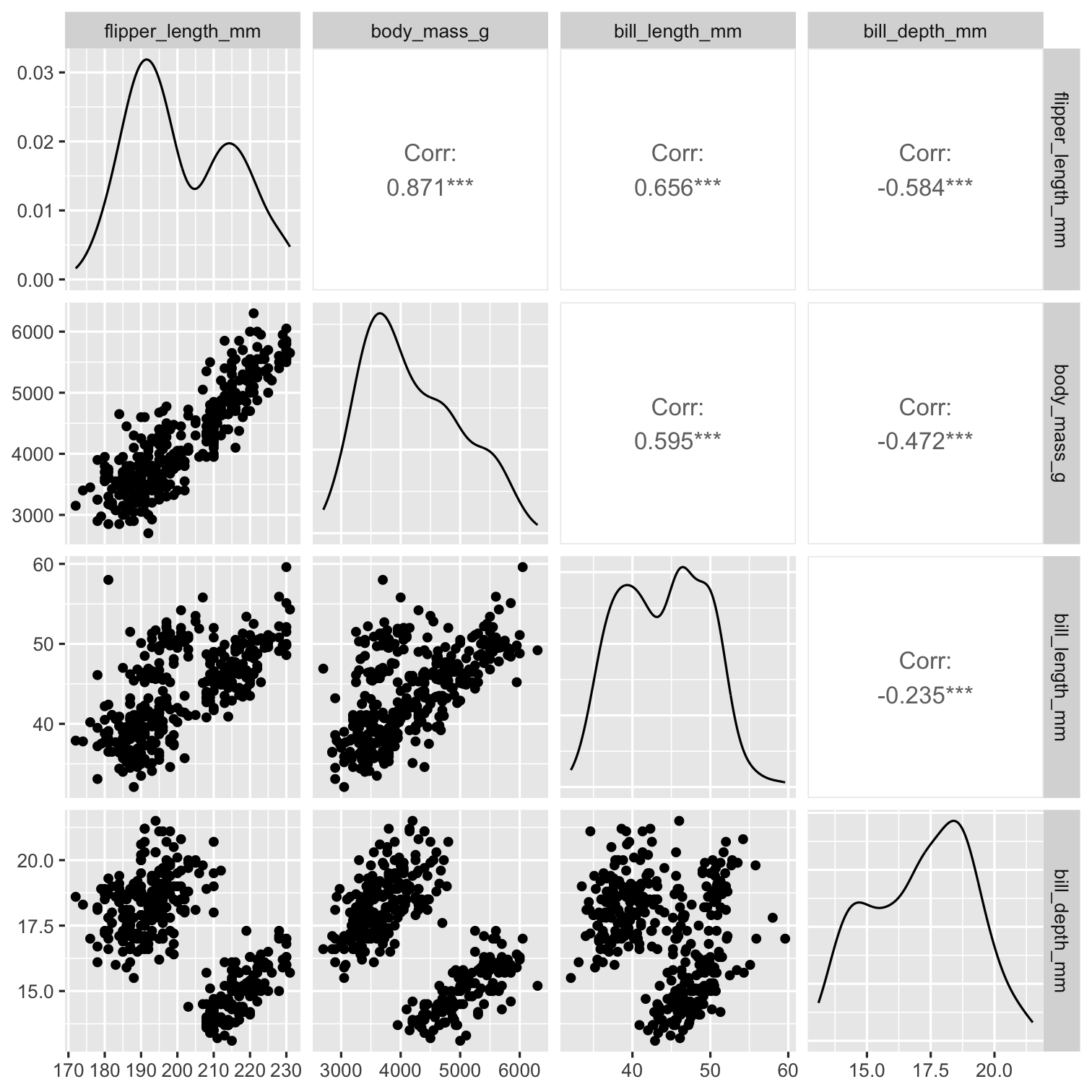
    )
```
]
]

.pull-right[
<img src="Slides_Part5_files/figure-html/unnamed-chunk-8-1.png" width="504" />
]

---

## Correlations between multiple variabeles visualized WITH COLOR!

.pull-left[

.footnotesize[

```r
penguins %>% 
  select(
    species,
    bill_depth_mm,
    bill_length_mm,
    flipper_length_mm,
    body_mass_g
  ) %>%
  ggpairs(
    aes(color = species),
    columns = c(
      "flipper_length_mm", "body_mass_g",
      "bill_length_mm", "bill_depth_mm")) +
  scale_colour_manual(
    values = c("darkorange","purple","cyan4")) +
  scale_fill_manual(
    values = c("darkorange","purple","cyan4"))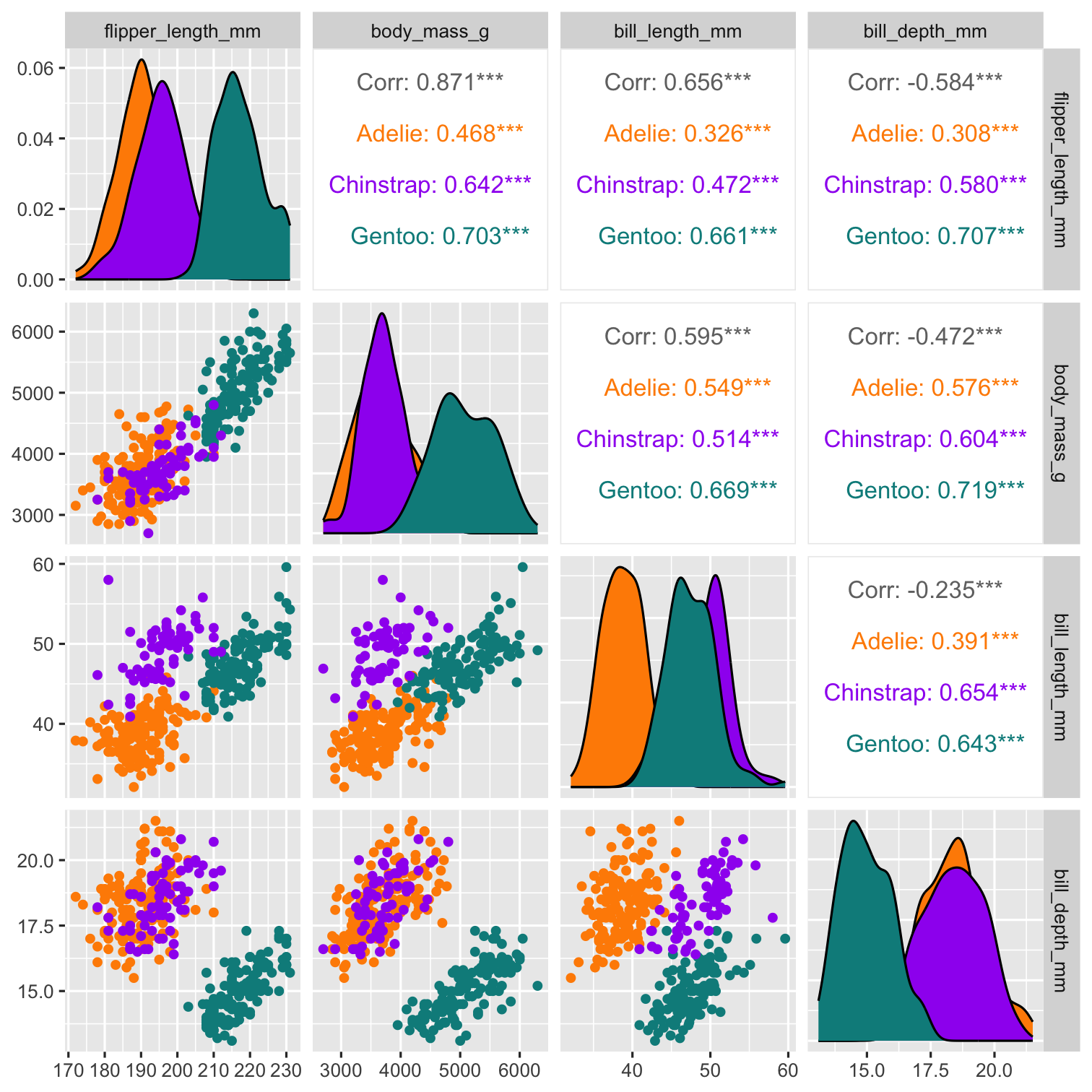
```
]
]

.pull-right[
<img src="Slides_Part5_files/figure-html/unnamed-chunk-10-1.png" width="504" />
]

---
class: inverse-green, center, middle
name: part2

# 2. t-test

---
## First some descriptives

.pull-left[
Compare Gentoo with Adelie penguins on `body_mass_g`

.footnotesize[

```r
library(kableExtra)
penguins %>% 
  select(
    species,
    body_mass_g
  ) %>%
  filter(
    species == 'Adelie' | species == 'Gentoo'
  ) %>%
  group_by(species) %>%
  summarize(
    count = n(),
    mean = mean(body_mass_g, na.rm = TRUE),
    sd = sd(body_mass_g, na.rm = TRUE)
  ) %>%
  kable()
```
]
]

.pull-right[

|species | count|     mean|       sd|
|:-------|-----:|--------:|--------:|
|Adelie  |   152| 3700.662| 458.5661|
|Gentoo  |   124| 5076.016| 504.1162|
]

---

## Create boxplots with `ggpubr` package

.pull-left[
.footnotesize[

```r
# install.packages(ggpubr)

library(ggpubr)
penguins %>% 
  select(
    species,
    body_mass_g
  ) %>%
  filter(
    species == 'Adelie' | species == 'Gentoo'
  ) %>%
  ggboxplot(
    x = "species", y = "body_mass_g", 
          color = "species", palette = c("#00AFBB", "#E7B800"),
        ylab = "Body Mass (g)", xlab = "Species")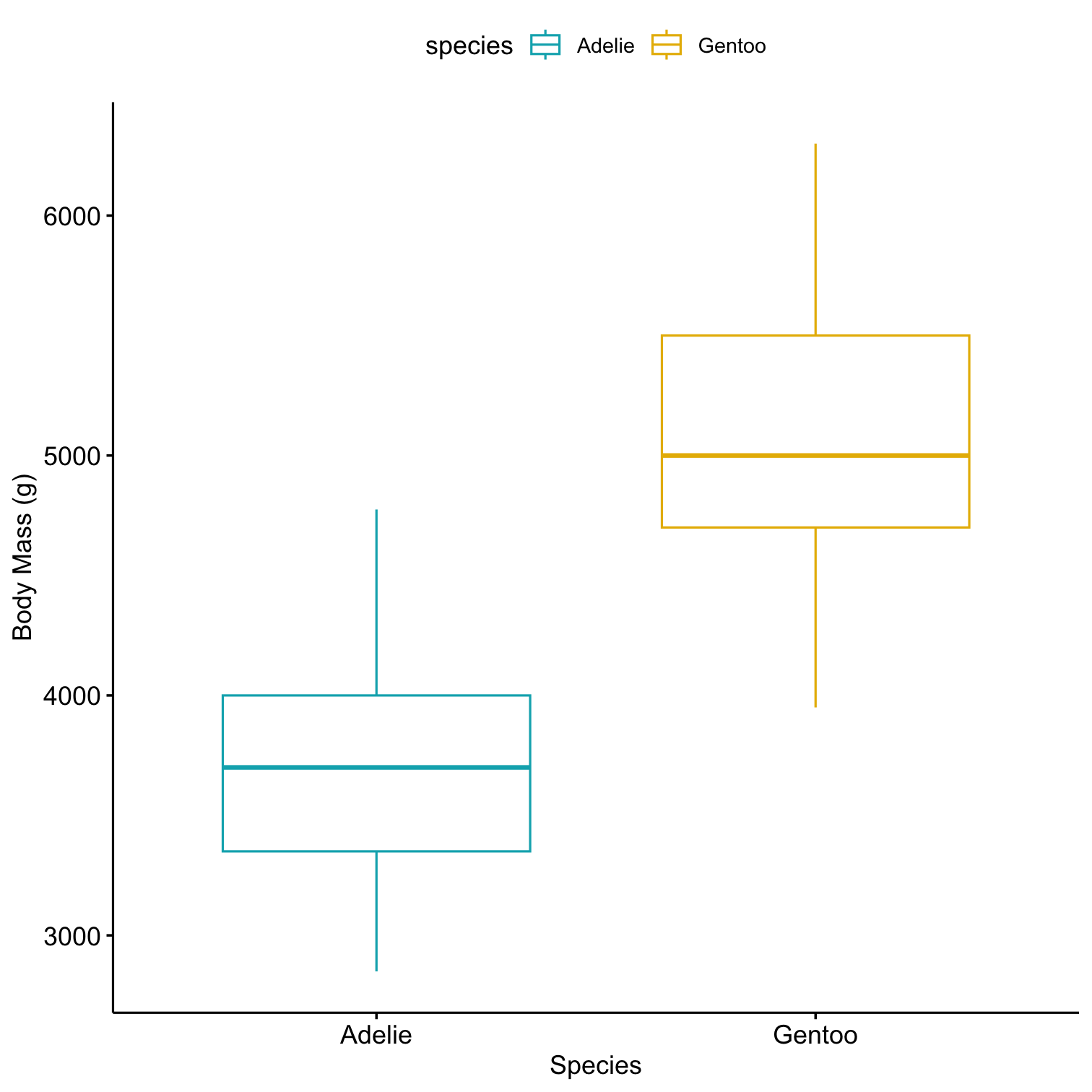
```
]
]

.pull-right[
<img src="Slides_Part5_files/figure-html/unnamed-chunk-14-1.png" width="504" />
]

---
## Checking the assumptions of equal variances with .UA-red[`var.test()`] function

.pull-left[
.footnotesize[

```r
p <- penguins %>% 
  select(
    species,
    body_mass_g
  ) %>%
  filter(
    species == 'Adelie' | species == 'Gentoo'
  )

var.test(body_mass_g ~ species, data= p)
```
]
]

.pull-right[

```
## 
## 	F test to compare two variances
## 
## data:  body_mass_g by species
## F = 0.82745, num df = 150, denom df = 122, p-value = 0.2691
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.5875588 1.1583164
## sample estimates:
## ratio of variances 
##          0.8274515
```
]

---
## Perform unpaired t-test with .UA-red[`t.test()`] function

.pull-left[
.footnotesize[

```r
p <- penguins %>% 
  select(
    species,
    body_mass_g
  ) %>%
  filter(
    species == 'Adelie' | species == 'Gentoo'
  )

t.test(body_mass_g ~ species, data= p, var.equal = TRUE)
```
]
]

.pull-right[

```
## 
## 	Two Sample t-test
## 
## data:  body_mass_g by species
## t = -23.614, df = 272, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group Adelie and group Gentoo is not equal to 0
## 95 percent confidence interval:
##  -1490.021 -1260.687
## sample estimates:
## mean in group Adelie mean in group Gentoo 
##             3700.662             5076.016
```
]

---
class: inverse-green, center, middle
name: part3

# 3. Linear regression

---

## .UA-red[`lm()`]

```r
Model1 <- lm(flipper_length_mm ~ body_mass_g, 
             data = penguins)
```

---

## Model results with .UA-red[`summary()`]

.footnotesize[

```r
summary(Model1)
```

```
## 
## Call:
## lm(formula = flipper_length_mm ~ body_mass_g, data = penguins)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -23.7626  -4.9138   0.9891   5.1166  16.6392 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 1.367e+02  1.997e+00   68.47   <2e-16 ***
## body_mass_g 1.528e-02  4.668e-04   32.72   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6.913 on 340 degrees of freedom
##   (2 observations deleted due to missingness)
## Multiple R-squared:  0.759,	Adjusted R-squared:  0.7583 
## F-statistic:  1071 on 1 and 340 DF,  p-value: < 2.2e-16
```
]

---
<div class="my-logo-right"> <img src="broom_logo.png" width="100%"/> </div>

## The .UA-red[`broom`]  package

Function: .UA-red[`tidy()`]

Result: tidy dataset with information on **parameter estimates**

```r
tidy(Model1, 
     conf.int = TRUE,
     conf.level = .90)
```

```
## # A tibble: 2 × 7
##   term        estimate std.error statistic   p.value conf.low conf.high
##   <chr>          <dbl>     <dbl>     <dbl>     <dbl>    <dbl>     <dbl>
## 1 (Intercept) 137.      2.00          68.5 5.71e-201 133.      140.    
## 2 body_mass_g   0.0153  0.000467      32.7 4.37e-107   0.0145    0.0160
```

---
<div class="my-logo-right"> <img src="broom_logo.png" width="100%"/> </div>

## The .UA-red[`broom`]  package + .UA-red[`kable()`]

```r
tidy(Model1, 
     conf.int = TRUE,
     conf.level = .90) %>%
  kable()
```

|term        |    estimate| std.error| statistic| p.value|    conf.low|   conf.high|
|:-----------|-----------:|---------:|---------:|-------:|-----------:|-----------:|
|(Intercept) | 136.7295593| 1.9968354|  68.47312|       0| 133.4360836| 140.0230350|
|body_mass_g |   0.0152759| 0.0004668|  32.72223|       0|   0.0145059|   0.0160459|

---
<div class="my-logo-right"> <img src="broom_logo.png" width="100%"/> </div>

## The .UA-red[`broom`] package

Function: .UA-red[`glance()`]

Result: tidy dataset with information on **model fit**

```r
glance(Model1)
```

```
## # A tibble: 1 × 12
##   r.squared adj.r.squared sigma statistic   p.value    df logLik   AIC   BIC
##       <dbl>         <dbl> <dbl>     <dbl>     <dbl> <dbl>  <dbl> <dbl> <dbl>
## 1     0.759         0.758  6.91     1071. 4.37e-107     1 -1146. 2297. 2309.
## # ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>
```

---
<div class="my-logo-right"> <img src="broom_logo.png" width="100%"/> </div>

## The .UA-red[`broom`] package

Function: .UA-red[`augment()`]

Result: add information to the dataset based on the model like **fitted values**, **residuals**, ...

```r
augment(Model1)
```

```
## # A tibble: 342 × 9
##    .rownames flipper_length_mm body_mass_g .fitted .resid    .hat .sigma .cooksd
##    <chr>                 <int>       <int>   <dbl>  <dbl>   <dbl>  <dbl>   <dbl>
##  1 1                       181        3750    194. -13.0  0.00385   6.89 6.88e-3
##  2 2                       186        3800    195.  -8.78 0.00366   6.91 2.97e-3
##  3 3                       195        3250    186.   8.62 0.00705   6.91 5.57e-3
##  4 5                       193        3450    189.   3.57 0.00550   6.92 7.41e-4
##  5 6                       190        3650    192.  -2.49 0.00431   6.92 2.81e-4
##  6 7                       181        3625    192. -11.1  0.00444   6.90 5.78e-3
##  7 8                       195        4675    208. -13.1  0.00395   6.89 7.19e-3
##  8 9                       193        3475    190.   3.19 0.00533   6.92 5.73e-4
##  9 10                      190        4250    202. -11.7  0.00293   6.89 4.19e-3
## 10 11                      186        3300    187.  -1.14 0.00663   6.92 9.14e-5
## # ℹ 332 more rows
## # ℹ 1 more variable: .std.resid <dbl>
```

---
<div class="my-logo-right"> <img src="broom_logo.png" width="100%"/> </div>

## The .UA-red[`broom`] package to check some assumptions

Functions: .UA-red[`augment()`] + .UA-red[`geom_histogram()`]

Result: Are the residuals normally distributed?

.pull-left[

```r
augment(Model1) %>% 
  select(.resid) %>% 
  ggplot(
    aes(
      x = .resid
    )
  ) + 
  geom_histogram() + 
  theme_minimal() +
  labs(
    title = "Model1",
    subtitle = "Distribution of residuals"
  ) +
  theme(plot.title.position = "plot")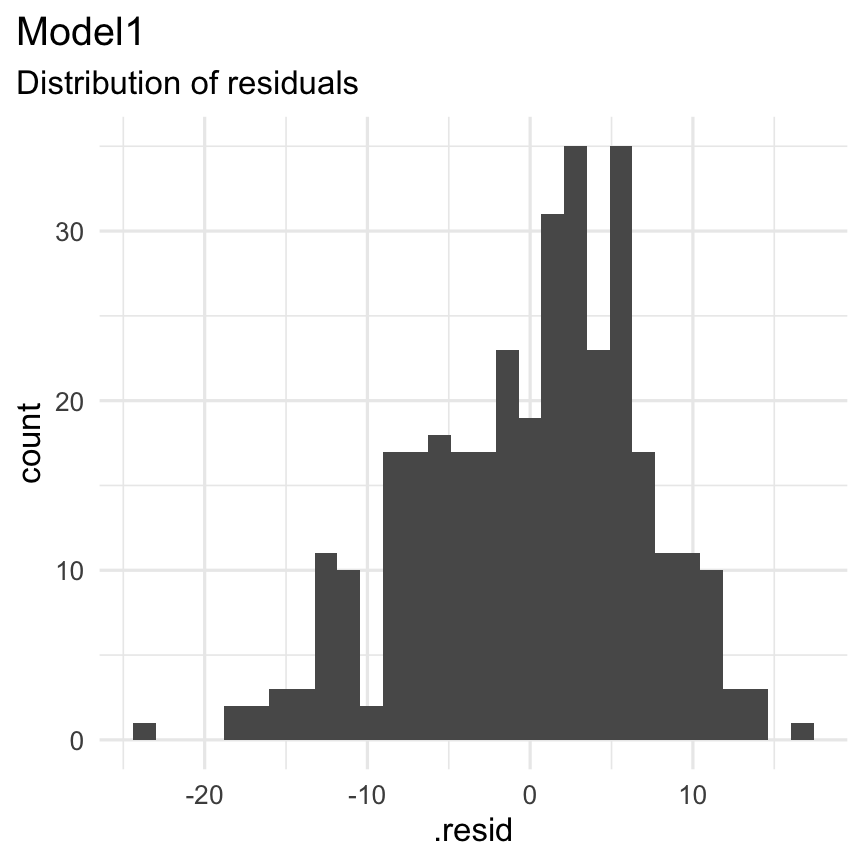
```
]

.pull-right[
<img src="Slides_Part5_files/figure-html/unnamed-chunk-27-1.png" width="288" style="display: block; margin: auto;" />
]

---
<div class="my-logo-right"> <img src="broom_logo.png" width="100%"/> </div>

## The .UA-red[`broom`] package to check some assumptions

Functions: .UA-red[`augment()`] + .UA-red[`geom_point()`]

Resultaat: Homoscedasticity?

.pull-left[

```r
augment(Model1) %>% 
  select(.fitted, .std.resid) %>% 
  ggplot(
    aes(
      x = .fitted,
      y = .std.resid
    )
  ) + 
  geom_point() + 
  theme_minimal() +
  labs(
    title = "Model1",
    subtitle = "Fitted values vs residuals"
  ) + geom_hline(yintercept = 0) +
  theme(plot.title.position = "plot")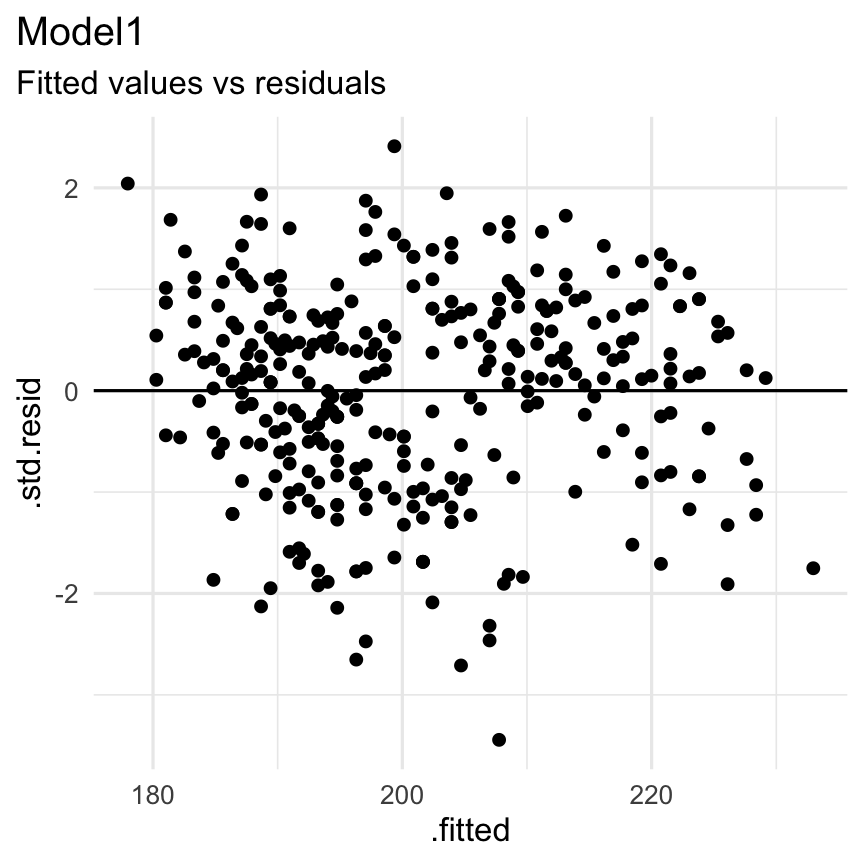
```
]

.pull-right[
<img src="Slides_Part5_files/figure-html/unnamed-chunk-29-1.png" width="288" style="display: block; margin: auto;" />
]

---
<div class="my-logo-right"> <img src="broom_logo.png" width="100%"/> </div>

## .UA-red[`broom`] package to visualise model results

Functions: .UA-red[`augment()`] + .UA-red[`geom_line()`]

Result: Plot of the fitted regression model (the line)

.pull-left[

```r
augment(Model1) %>% 
  select(.fitted, body_mass_g) %>% 
  ggplot(
    aes(
      x = body_mass_g,
      y = .fitted
    )
  ) + 
  geom_line() + 
  theme_minimal() +
  labs(
    title = "Model1",
    subtitle = "Fitted values based on body mass",
    x = "body mass (g)",
    y = "fitted values"
  )  +
  theme(plot.title.position = "plot")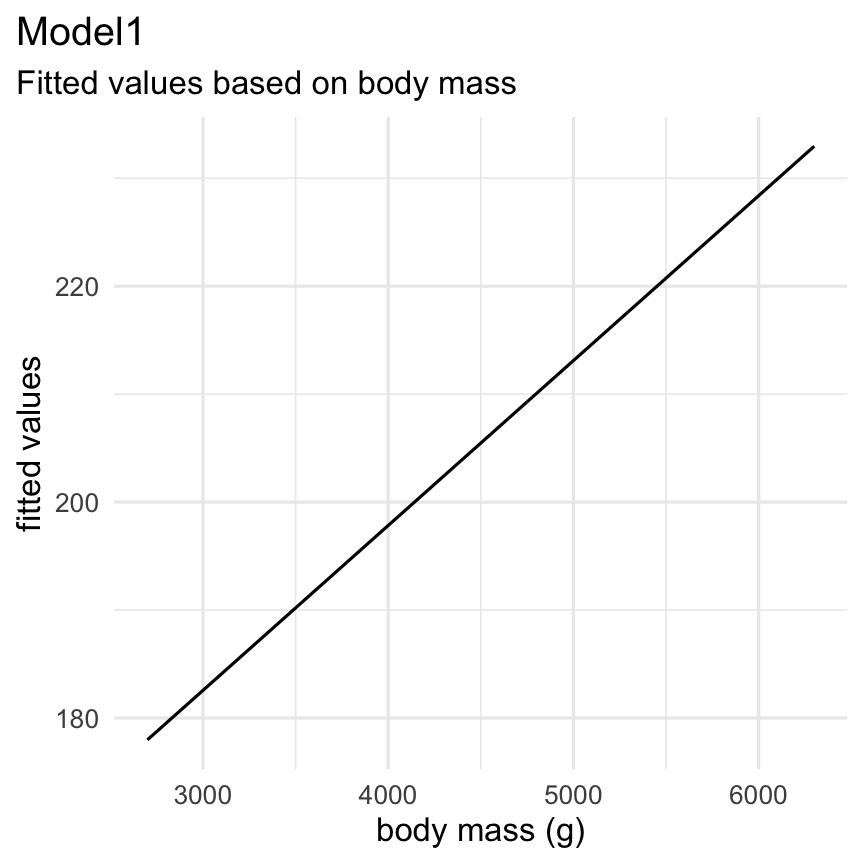
```
]

.pull-right[
<img src="Slides_Part5_files/figure-html/unnamed-chunk-31-1.png" width="288" style="display: block; margin: auto;" />
]

---

## Multivariate regression

.footnotesize[

```r
Model2 <- lm(
  flipper_length_mm ~ body_mass_g + sex + species,
  data = penguins
)

tidy(Model2) %>%
  kable()
```

|term             |    estimate| std.error| statistic|   p.value|
|:----------------|-----------:|---------:|---------:|---------:|
|(Intercept)      | 164.5887169| 3.1836146| 51.698694| 0.0000000|
|body_mass_g      |   0.0065499| 0.0009308|  7.036742| 0.0000000|
|sexmale          |   2.4777215| 0.8540581|  2.901116| 0.0039696|
|speciesChinstrap |   5.5444400| 0.7852051|  7.061136| 0.0000000|
|speciesGentoo    |  18.0213174| 1.4424942| 12.493165| 0.0000000|
]

---

## Model comparison

Model fit of multiple models:

```r
M1_info <- glance(Model1) %>% select(r.squared, AIC, BIC)
M2_info <- glance(Model2) %>% select(r.squared, AIC, BIC)

M1_info %>% rbind(M2_info) %>% kable()
```

| r.squared|      AIC|      BIC|
|---------:|--------:|--------:|
| 0.7589925| 2297.035| 2308.540|
| 0.8562944| 2068.357| 2091.206|

---

## Visualize this model

.pull-left[
.footnotesize[

```r
augment(Model2) %>%
  ggplot() +
  geom_point(
    aes(x = body_mass_g,
        y = flipper_length_mm,
        color = sex),
    alpha = .6
  ) +
  geom_line(
    aes(
      x = body_mass_g,
      y = .fitted,
      color = sex,
    ),
    size = 1.5
  ) +
  facet_wrap(.~species) +
  theme_minimal()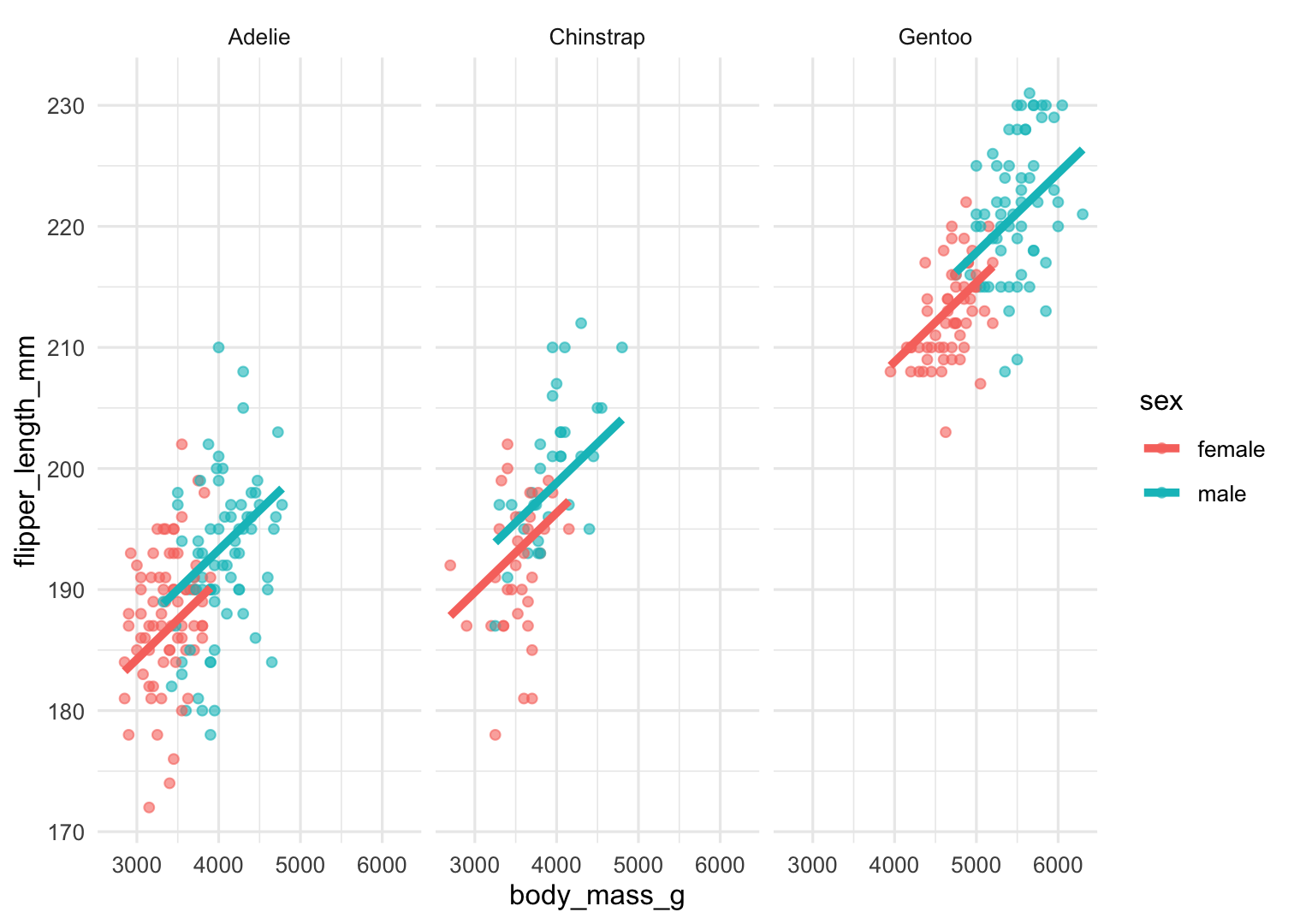
```
]
]

.pull-right[
<img src="Slides_Part5_files/figure-html/unnamed-chunk-35-1.png" width="504" style="display: block; margin: auto;" />
]

---

## Some cool stuff with the .UA-red[`sjplot`] package

For instance, create an html-table with the estimates of two models: Model1 & Model2

Function: .UA-red[`tab_model()`]

```r
library(sjPlot)
tab_model(Model1, Model2)
```

<table style="border-collapse:collapse; border:none;">
<tr>
<th style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm;  text-align:left; ">&nbsp;</th>
<th colspan="3" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">flipper length mm</th>
<th colspan="3" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">flipper length mm</th>
</tr>
<tr>
<td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal;  text-align:left; ">Predictors</td>
<td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal;  ">Estimates</td>
<td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal;  ">CI</td>
<td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal;  ">p</td>
<td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal;  ">Estimates</td>
<td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal;  ">CI</td>
<td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal;  col7">p</td>
</tr>
<tr>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">(Intercept)</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  ">136.73</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  ">132.80&nbsp;&ndash;&nbsp;140.66</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  "><strong>&lt;0.001</strong></td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  ">164.59</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  ">158.33&nbsp;&ndash;&nbsp;170.85</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  col7"><strong>&lt;0.001</strong></td>
</tr>
<tr>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">body mass g</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  ">0.02</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  ">0.01&nbsp;&ndash;&nbsp;0.02</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  "><strong>&lt;0.001</strong></td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  ">0.01</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  ">0.00&nbsp;&ndash;&nbsp;0.01</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  col7"><strong>&lt;0.001</strong></td>
</tr>
<tr>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">sex [male]</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  "></td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  "></td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  "></td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  ">2.48</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  ">0.80&nbsp;&ndash;&nbsp;4.16</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  col7"><strong>0.004</strong></td>
</tr>
<tr>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">species [Chinstrap]</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  "></td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  "></td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  "></td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  ">5.54</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  ">4.00&nbsp;&ndash;&nbsp;7.09</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  col7"><strong>&lt;0.001</strong></td>
</tr>
<tr>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">species [Gentoo]</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  "></td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  "></td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  "></td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  ">18.02</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  ">15.18&nbsp;&ndash;&nbsp;20.86</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center;  col7"><strong>&lt;0.001</strong></td>
</tr>
<tr>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm; border-top:1px solid;">Observations</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="3">342</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="3">333</td>
</tr>
<tr>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm;">R<sup>2</sup> / R<sup>2</sup> adjusted</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="3">0.759 / 0.758</td>
<td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="3">0.856 / 0.855</td>
</tr>

</table>

---

## Some cool stuff with the .UA-red[`sjplot`] package

Create a plot of predicted values based on the effect of body_mass_g

Function: .UA-red[`plot_model()`] with `type = "pred"` specifically to plot **predicted values**

.pull-left[

```r
plot_model(Model2, 
           type = "pred", 
           terms = "body_mass_g")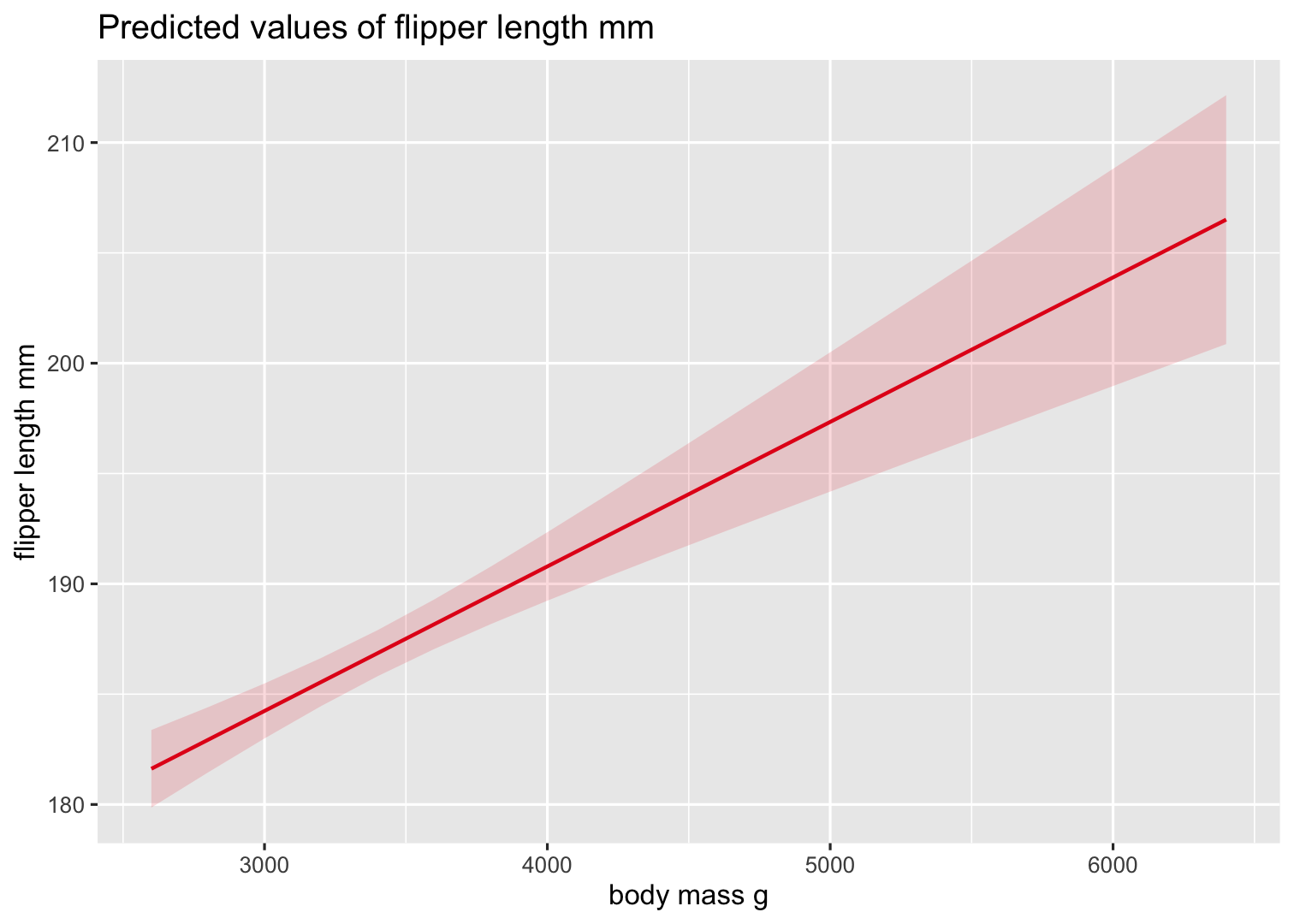
```
]

.pull-right[
<img src="Slides_Part5_files/figure-html/unnamed-chunk-38-1.png" width="504" style="display: block; margin: auto;" />
]
---

## Some cool stuff with the .UA-red[`sjplot`] package

Function: .UA-red[`plot_model()`] creates a **ggplot object**! So we can customize it!

.pull-left[

```r
plot_model(Model2, 
           type = "pred", 
           terms = "body_mass_g") +
  theme_minimal()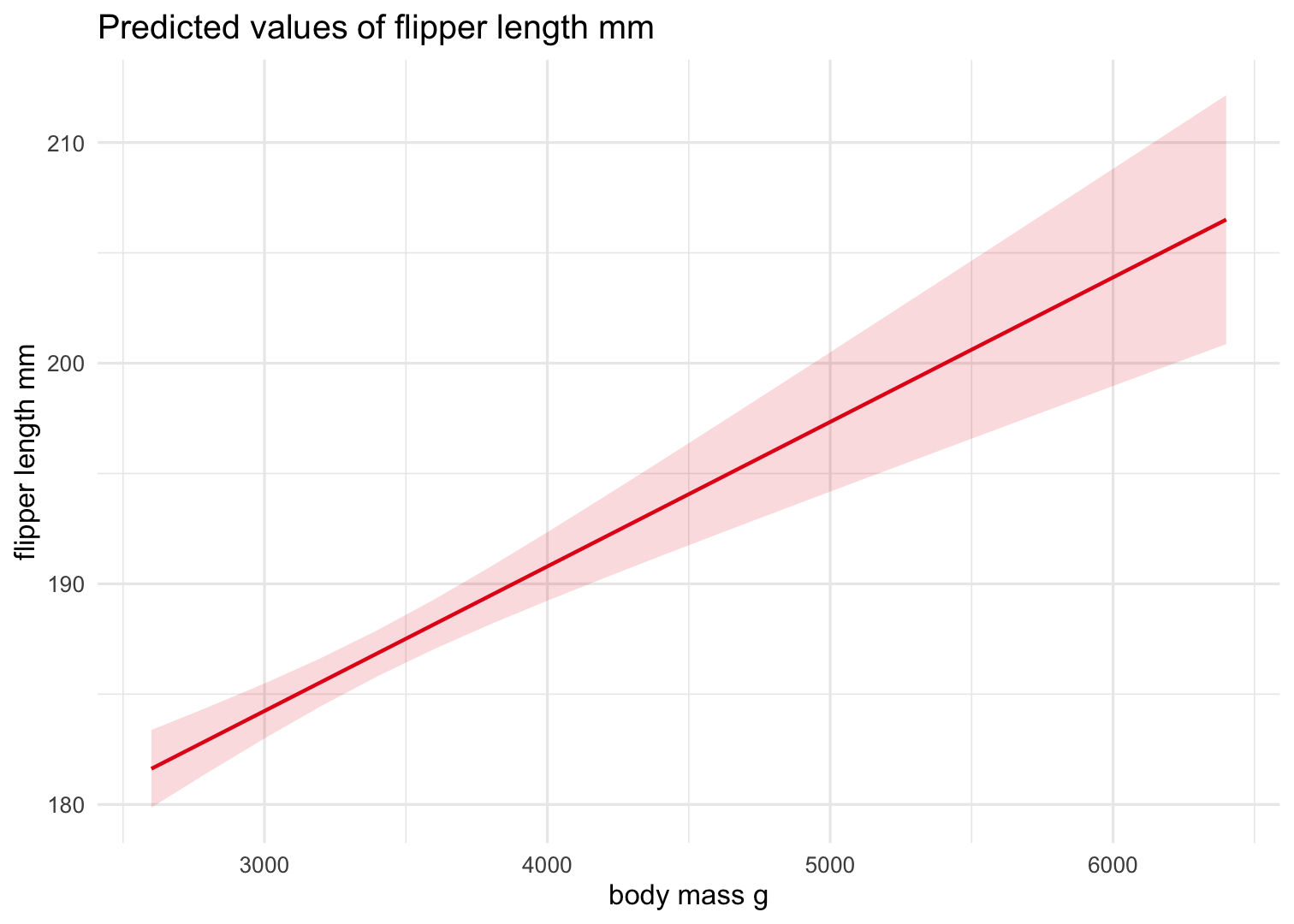
```
]

.pull-right[
<img src="Slides_Part5_files/figure-html/unnamed-chunk-40-1.png" width="504" style="display: block; margin: auto;" />
]
---
## Some cool stuff with the .UA-red[`sjplot`] package

Create a plot of the different parameter estimates in the model

Function: .UA-red[`plot_model()`] without a `type = pred` argument

.pull-left[

```r
plot_model(Model2) +
  theme_minimal()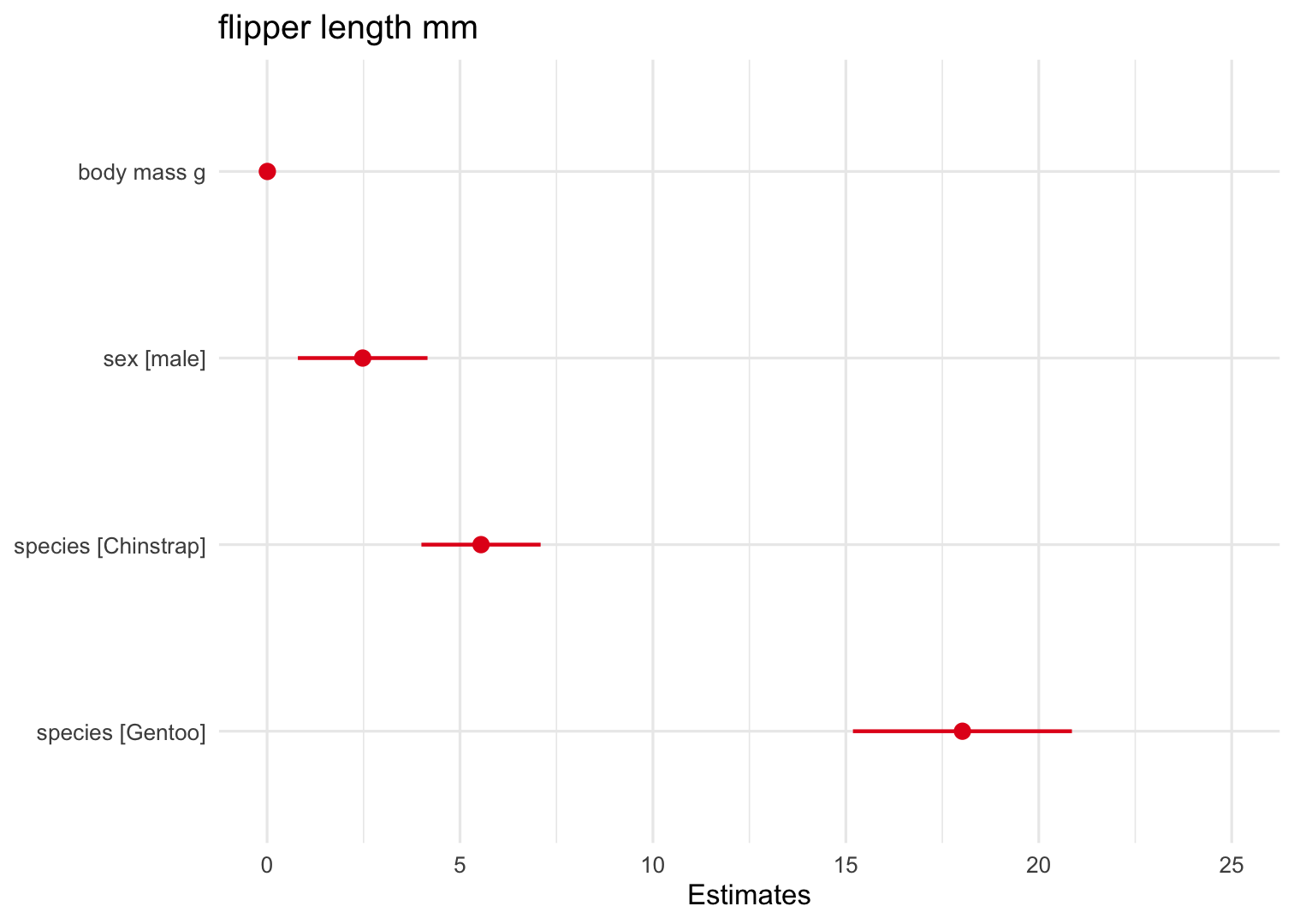
```
]

.pull-right[
<img src="Slides_Part5_files/figure-html/unnamed-chunk-42-1.png" width="504" style="display: block; margin: auto;" />
]
---
##Other Statistical Modelling in R

Structural Equation Modelling: `lavaan`

Multilevel analyses: `lme4`

Cluster Analyses: `mclust`

Factor Analyses (or PCA) & reliability analyses (e.g., Cronbach's alpha): `psych`

Item Response Theory models: `ltm` or `sirt` or `mirt`

Bayesian analyses (using MCMC): `brms`